Understanding our Earth
We are a world-leading independent research organisation providing objective, expert geoscientific data, information and knowledge.
Latest news and events

‘Three norths’ set to leave England and not return for hundreds of years
12/12/2025
The historic alignment of true, magnetic, and grid north is set to leave England, three years after they combined in the country for the first time since records began.

BGS agrees to establish collaboration framework with Ukrainian government
11/12/2025
The partnership will focus on joint research and data exchange opportunities with Ukrainian colleagues.

Making research matter: BGS joins leading research organisations in new national initiative
10/12/2025
A new alliance of 35 organisations has been formed that is dedicated to advancing science for the benefit of people, communities, the economy and national priorities.

New 3D model to help mitigate groundwater flooding
08/12/2025
BGS has released a 3D geological model of Gateshead to enhance understanding of groundwater and improve the response to flooding.

Scientists gain access to ‘once in a lifetime’ core from Great Glen Fault
01/12/2025
The geological core provides a cross-section through the UK’s largest fault zone, offering a rare insight into the formation of the Scottish Highlands.

New research shows artificial intelligence earthquake tools forecast aftershock risk in seconds
25/11/2025
Researchers from BGS and the universities of Edinburgh and Padua created the forecasting tools, which were trained on real earthquakes around the world.

BGS welcomes publication of the UK Critical Minerals Strategy
23/11/2025
A clear strategic vision for the UK is crucial to secure the country’s long-term critical mineral supply chains and drive forward the Government’s economic growth agenda.

New funding awarded for UK geological storage research
21/11/2025
A project that aims to investigate the UK’s subsurface resource to support net zero has been awarded funding and is due to begin its research.

How the geology on our doorstep can help inform offshore infrastructure design
19/11/2025
BGS is part of a new collaboration using onshore field work to contextualise offshore data and update baseline geological models which can inform the sustainable use of marine resources.

UK braced for what could be the largest solar storm in over two decades
12/11/2025
Intense geomagnetic activity could disrupt technology such as communication systems, global positioning systems and satellite orbits.

First distributed acoustic sensing survey completed at UK Geoenergy Observatory
12/11/2025
New research at the Cheshire Observatory has shown the potential for mapping thermal changes in the subsurface using sound waves.
Latest BGS Geology 50K mapping data launched
06/11/2025
Some of our most widely used maps have received a major update, including the 1:50 000-scale map series that now includes enhanced coverage of Great Britain.
Our core challenge areas

Decarbonisation and resource management
Decarbonisation of power production, heat, transport and industry is a major challenge and one that intrinsically involves geoscience.

Multi-hazards and resilience
We work with partners worldwide to enhance understanding of hazards, vulnerability, exposure and risk to ensure our science is useful, usable and used.

International geoscience
BGS is active across the globe delivering institutional strengthening programmes and applied research projects across a wide variety of sectors.

National geoscience
The National Geoscience programme is a forward-looking investment in UK geology that provides relevant, coherent and enriched geoscience knowledge for our stakeholders.

Digital geoscience
The BGS is a data-rich organisation. Our data science and data infrastructure are fundamental to our future research and underpin our strategic challenges.
Map viewers
Data published through map viewers allowing you to reveal more about the ground beneath your feet.

Technologies
Applications, software and online services created by the BGS and our collaborators.

Information hub
Data collections, publications, scanned records and other data gathered by BGS and provided by external organisations.
OpenGeoscience
Accessing maps and downloading data, scans, photos and other information via BGS’s free OpenGeoscience service.

Digital geoscience
The BGS is a data-rich organisation. Our data science and data infrastructure are fundamental to our future research and underpin our strategic challenges.
Digital data licensing and resellers
Providing a wide range of licences for the use and utilisation of our information products by for those interested in an information product and the Open Government Licence is not applicable.

National Geoscience Data Centre
Collecting and preserving geoscientific data, making it available to a wide range of users and communities.

National Geological Repository
Hosting BGS’s collections of borehole cores, cuttings, samples, specimens, and related subsurface information from the UK landmass and continental shelf.

Discovering Geology
Discovering Geology introduces a range of geoscience topics to school-age students and learners of all ages. Explore these pages to discover the fascinating processes and properties that shape our dynamic planet.

Rocks and minerals
Find out more about the differences between rocks and minerals and how they are formed.

Discovering Geology: climate change
What is the difference between weather and climate? what causes the Earth’s climate to change and what are the impacts? Find out more with our Discovery Geology climate change resources.

Earth hazards
The Earth beneath our feet is constantly shifting and moving, and violently with catastrophic and immediate results. Find out more about earth hazards.

Geological processes
Planet Earth is dynamic with a surface that is always changing. Find out about the processes that cause these changes.
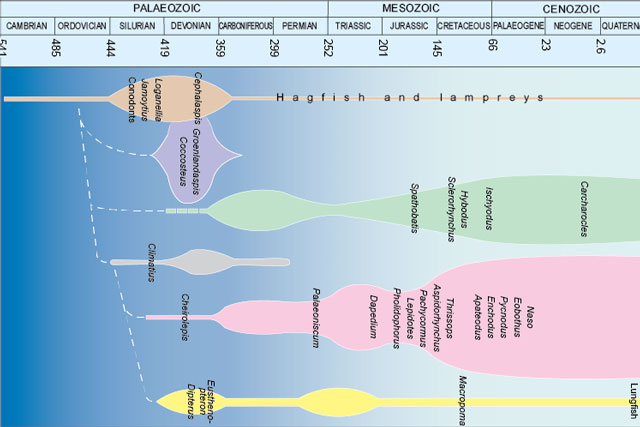
Fossils and geological time
Take a look at the history of the Earth, from its formation over four and a half billion years ago to present times.

About BGS
As the national geological survey, we are the UK’s premier provider of objective and authoritative scientific data, information and knowledge to help society understand our Earth.

Our data and services
The BGS offers a range of services and information for businesses, home-owners, policymakers and the general public.

Working with us
BGS is committed to being an employer of choice and strives to embrace a culture of inclusivity and flexibility.

Offices and locations
Find out more about our offices and facilities located across the UK.

Contact us
Find out more about the BGS and the services we offer through our enquiries and customer services team.